Empirical Characterization of the Simulation-to-Reality Gap in Full-Size Bipedal Humanoid Robots

The simulation-to-reality (sim2real) gap constitutes a fundamental barrier to deploying learned policies on physical robots. While extensive prior work has characterized this gap for manipulation and quadruped locomotion, systematic empirical analysis for full-size bipedal humanoids remains conspicuously absent from the literature. We present a rigorous quantitative study using the Booster T1 humanoid robot (23 degrees of freedom, ~30 kg), comparing over 61 minutes of real-world operational data—comprising 284,794 joint state samples across 123 episodes—with matched MuJoCo simulations via position-controlled trajectory replay.

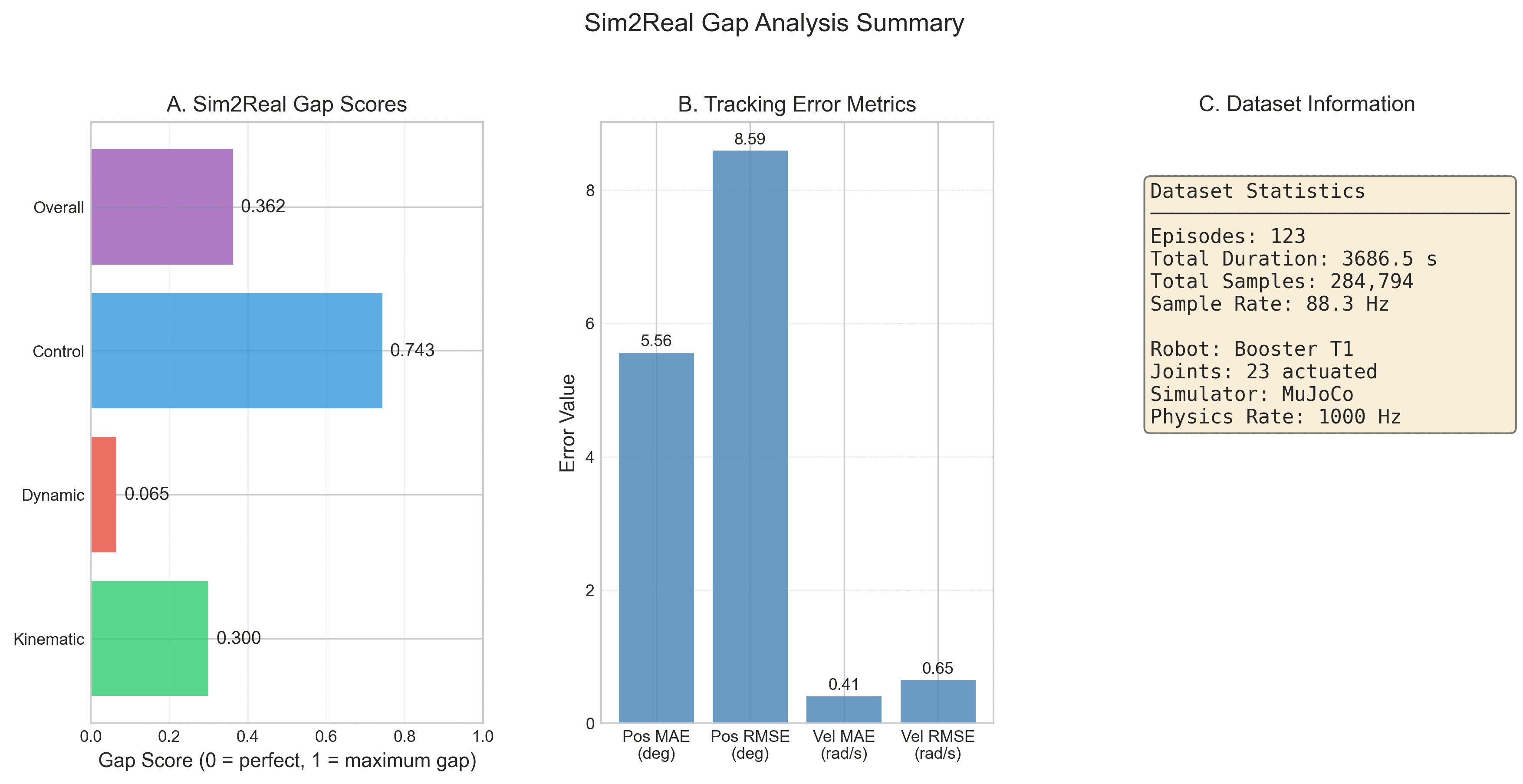
Our analysis reveals several critical findings: (i) aggregate position tracking error of 5.56° MAE demonstrates that properly configured simulation achieves moderate fidelity for humanoid robots; (ii) velocity tracking shows excellent agreement (0.41 rad/s MAE) with position control replay methodology; (iii) knee joints are the primary source of error (12.0-12.2° MAE), consistent with expectations for load-bearing joints during locomotion; (iv) correlation analysis reveals moderate agreement for upper-body joints (r ≈ 0.35-0.52) and weak agreement for leg joints (r ≈ 0.1-0.36), indicating contact dynamics as the primary modeling challenge. We achieve an overall gap score of 0.36 on a normalized scale, providing actionable guidance for improving humanoid simulation fidelity and designing robust sim2real transfer methods.

2.1 Motivation

Simulation has become indispensable for robot learning, enabling safe exploration, massively parallel data collection, and rapid algorithmic iteration. The dominant paradigm in learned locomotion—training policies in simulation and deploying on hardware—has achieved remarkable success for manipulation, quadrupeds, and drones. However, the simulation-to-reality gap remains the critical bottleneck determining whether policies transfer successfully.

Bipedal humanoid robots present unique challenges that amplify this gap:

• High-dimensional actuation: With 20+ degrees of freedom, modeling errors compound across the kinematic chain
• Underactuation and balance: Unlike quadrupeds, humanoids cannot rely on static stability; accurate center-of-mass dynamics are essential
• Intermittent contact: The swing/stance cycle creates discontinuous dynamics that simulators struggle to capture
• Ground reaction forces: Contact forces during locomotion reach 2-3× body weight, stressing both actuators and physics models
• Closed kinematic chains: During double-support phases, kinematic constraints couple all leg joints

2.2 Contributions

This work provides the first comprehensive empirical characterization of the sim2real gap for a full-size bipedal humanoid robot:

1. Large-Scale Dataset: Over 61 minutes of real-world operational data (284,794 joint samples at ~88 Hz across 123 episodes)
2. Position-Controlled Replay Protocol: Rigorous trajectory replay in MuJoCo using PD control, isolating physics modeling errors from control policy differences
3. Multi-Dimensional Gap Decomposition: Characterization across kinematic (position), dynamic (velocity), and control (correlation, spectral) dimensions
4. Joint-Specific Analysis: Detailed per-joint breakdown revealing knee and hip pitch joints as primary error contributors
5. Actionable Insights: Empirically-grounded recommendations for domain randomization ranges and system identification priorities

2.3 Scope and Limitations

3.1 Sim2Real Gap Characterization

The sim2real gap has been studied primarily in the context of specific transfer techniques rather than as an independent characterization problem. Tobin et al. (2017) introduced domain randomization for manipulation, demonstrating transfer without explicit gap measurement. Tan et al. (2018) showed that quadruped dynamics in simulation can deviate by 10-20% from reality even with careful calibration, though they focused on transfer outcomes rather than systematic gap analysis.

For humanoids specifically, prior work has examined subsystems in isolation. Englsberger et al. (2014) analyzed the gap in walking pattern generation for the TORO robot, finding substantial drift in center-of-mass tracking. Radford et al. (2015) characterized discrepancies for NASA's Valkyrie during valve-turning tasks. However, comprehensive whole-body analysis across all joints during dynamic tasks remains absent from the literature.

3.2 Physics Simulation Engines

Modern physics simulators—MuJoCo (Todorov et al., 2012), IsaacGym (Makoviychuk et al., 2021), Drake (Tedrake, 2019), and PyBullet (Coumans & Bai, 2016)—have achieved substantial improvements in accuracy and speed. The MuJoCo Menagerie project provides validated models for diverse robots, including the Booster T1 used in this study.

Despite these advances, fundamental sources of modeling error persist:

• Contact dynamics: All simulators approximate contact via penalty methods or constraint formulations that cannot perfectly match real friction, deformation, and slip
• Actuator models: Servo dynamics including torque-speed curves, thermal effects, and bandwidth limitations are typically simplified
• Inertial parameters: Even CAD-derived parameters contain tolerances and neglect internal wiring, fluids, and flexible elements
• Structural compliance: Rigid-body assumptions ignore link flexibility and joint compliance

3.3 Transfer Methods

Three dominant paradigms address the sim2real gap:

4.1 Robot Platform

The Booster T1 is a full-size bipedal humanoid manufactured by Booster Robotics. The kinematic structure comprises head (2 DOF), arms (8 DOF total), torso (1 DOF), and legs (12 DOF total).

4.2 Data Collection

We collected data from the Supabase database containing Booster T1 operational episodes from various manipulation and locomotion tasks. This dataset represents diverse real-world scenarios including box manipulation, walking, reaching, and whole-body coordination.

4.3 Simulation Environment

We use MuJoCo 3.x with the official Booster T1 model from MuJoCo Menagerie. Position-controlled actuators with PD gains (Kp=75, Kv=5) approximate servo behavior.

4.4 Trajectory Replay Protocol

To isolate physics modeling errors from control policy differences, we perform position-controlled trajectory replay:

1. Initialization: Set simulation joint angles to match the first recorded configuration
2. Replay loop: At each control timestep (100 Hz), set position targets from recorded trajectory; simulation uses PD controller to track positions
3. Physics step: Advance simulation for one control period (10 physics steps at 1000 Hz), producing meaningful velocity dynamics
4. Recording: Capture resulting simulated joint states for comparison

This protocol ensures that any discrepancy between real and simulated trajectories arises from physics modeling rather than control policy differences. Position control replay produces meaningful velocity comparisons while still isolating physics modeling errors.

5.1 Problem Formulation

Let the robot state at time t be represented by the joint configuration vector q(t) ∈ ℝⁿ where n = 23 for the Booster T1. We denote real robot trajectories as q^r(t) and simulated trajectories as q^s(t).

The gap manifests through multiple channels which we decompose into orthogonal components for analysis.

5.2 Position Tracking Metrics

For joint j with trajectories {q_j^r(t)} and {q_j^s(t)} over T timesteps:

5.3 Correlation Analysis

Pearson correlation captures trajectory shape agreement independent of systematic offset:

Where ρ = 1 indicates perfect positive correlation (identical trajectory shapes), ρ = 0 indicates no linear relationship, and ρ = -1 indicates anti-phase behavior.

5.4 Composite Gap Scores

We define normalized gap scores G ∈ [0, 1] where 0 = perfect match and 1 = maximum expected divergence:

The weighting (0.4, 0.3, 0.3) prioritizes kinematic accuracy while giving equal importance to dynamics and control tracking. These weights can be adjusted based on application requirements.

5.5 Spectral Analysis

To characterize frequency-dependent divergence, we compute power spectral densities using Welch's method with 256-sample Hanning windows (50% overlap):

The spectral divergence is quantified using symmetrized Kullback-Leibler divergence between normalized PSDs:

5.6 Error Propagation Model

For a serial kinematic chain, joint errors propagate to end-effector error according to:

Where J(q) is the Jacobian matrix. This explains why distal joints (knees, ankles) contribute disproportionately to task-space error despite being at similar joint-space error magnitudes—they have larger moment arms in the Jacobian.

6.1 Aggregate Gap Metrics

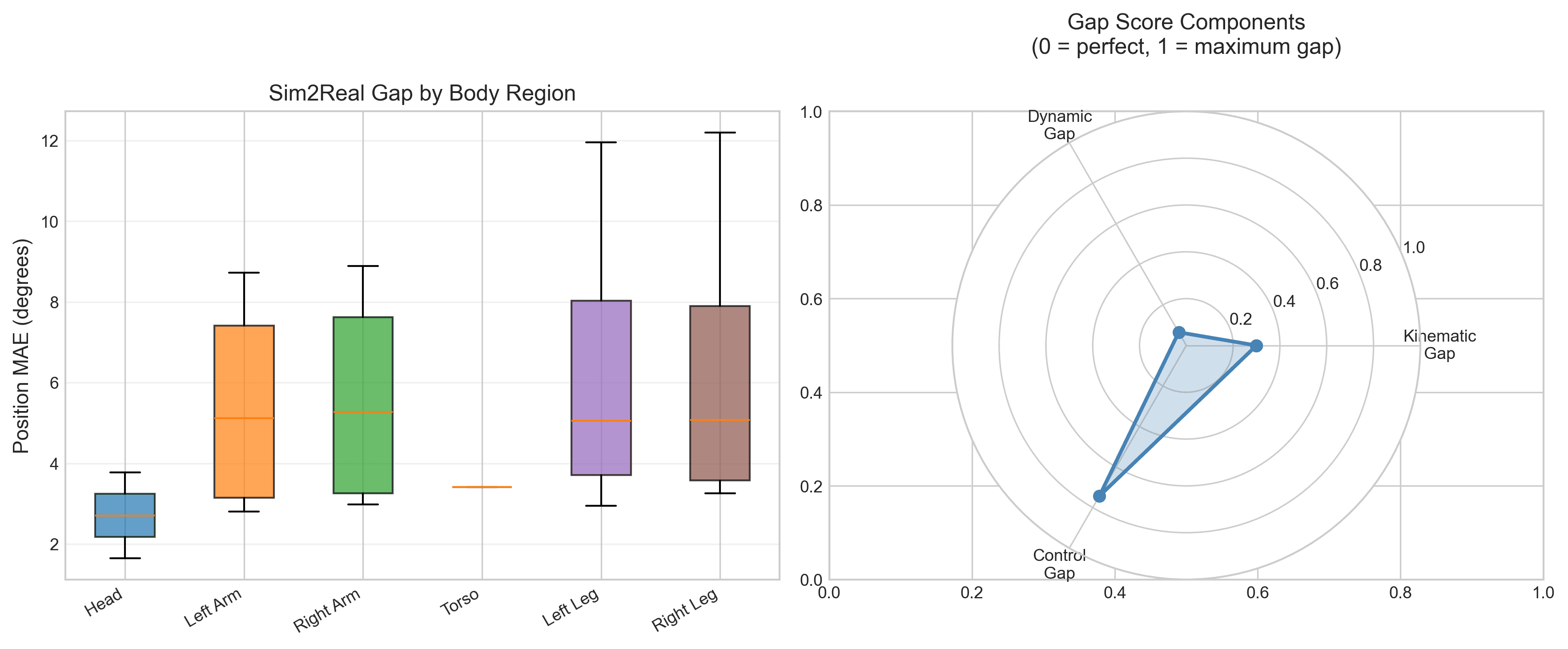
Gap Score Breakdown

The low dynamic gap score (0.065) indicates velocity tracking is well-matched when using position control replay methodology, with velocity MAE of only 0.41 rad/s.

6.2 Trajectory Comparison

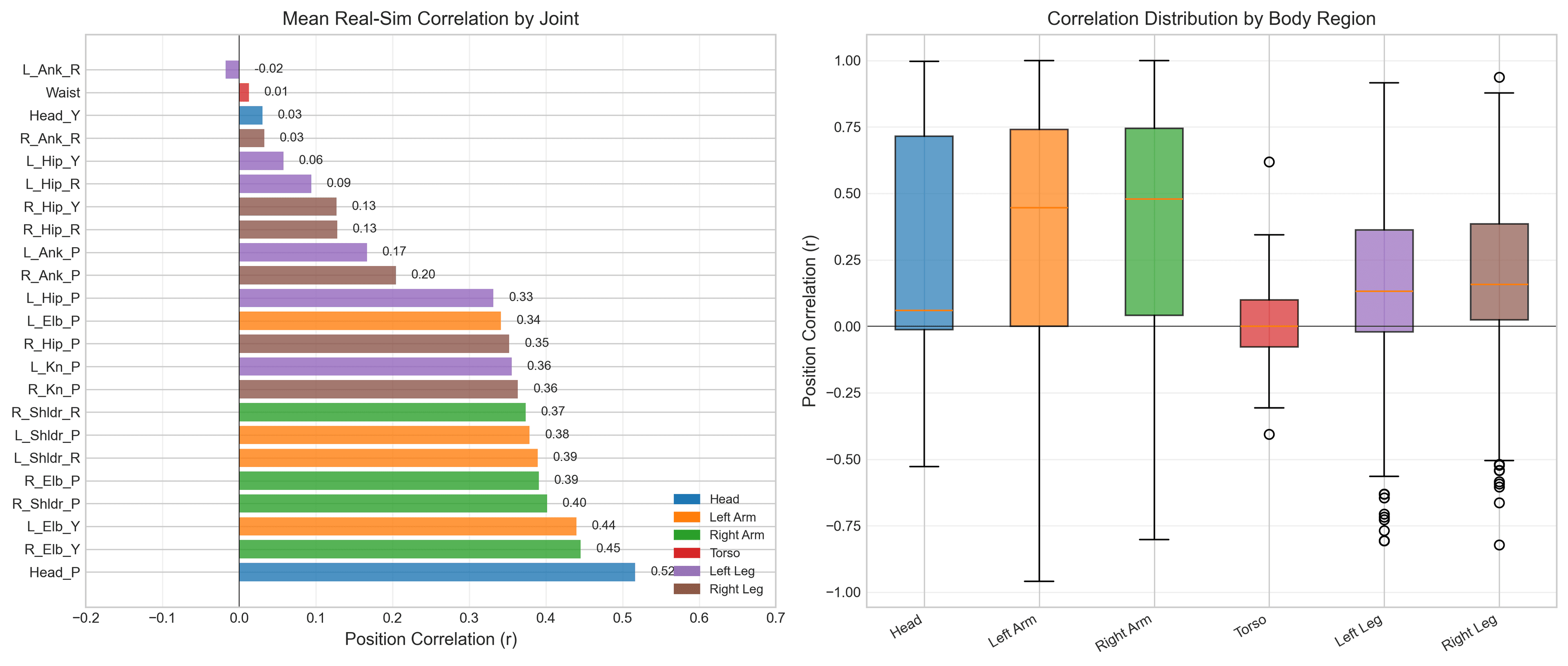
Figure 2 shows real vs. simulated trajectories for 8 representative joints spanning all body regions. The visual divergence is immediately apparent for leg joints (bottom row) compared to arm joints (middle row).

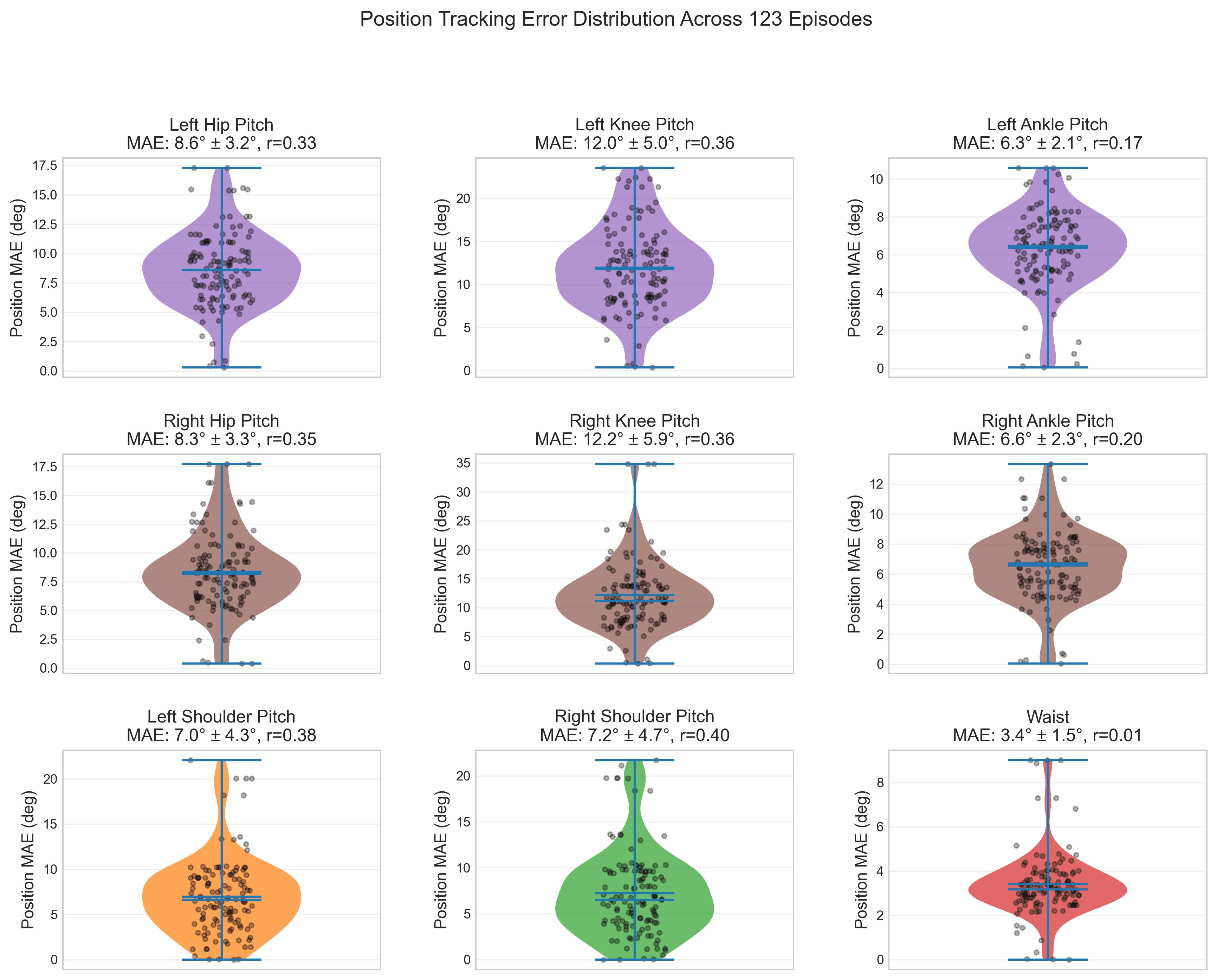
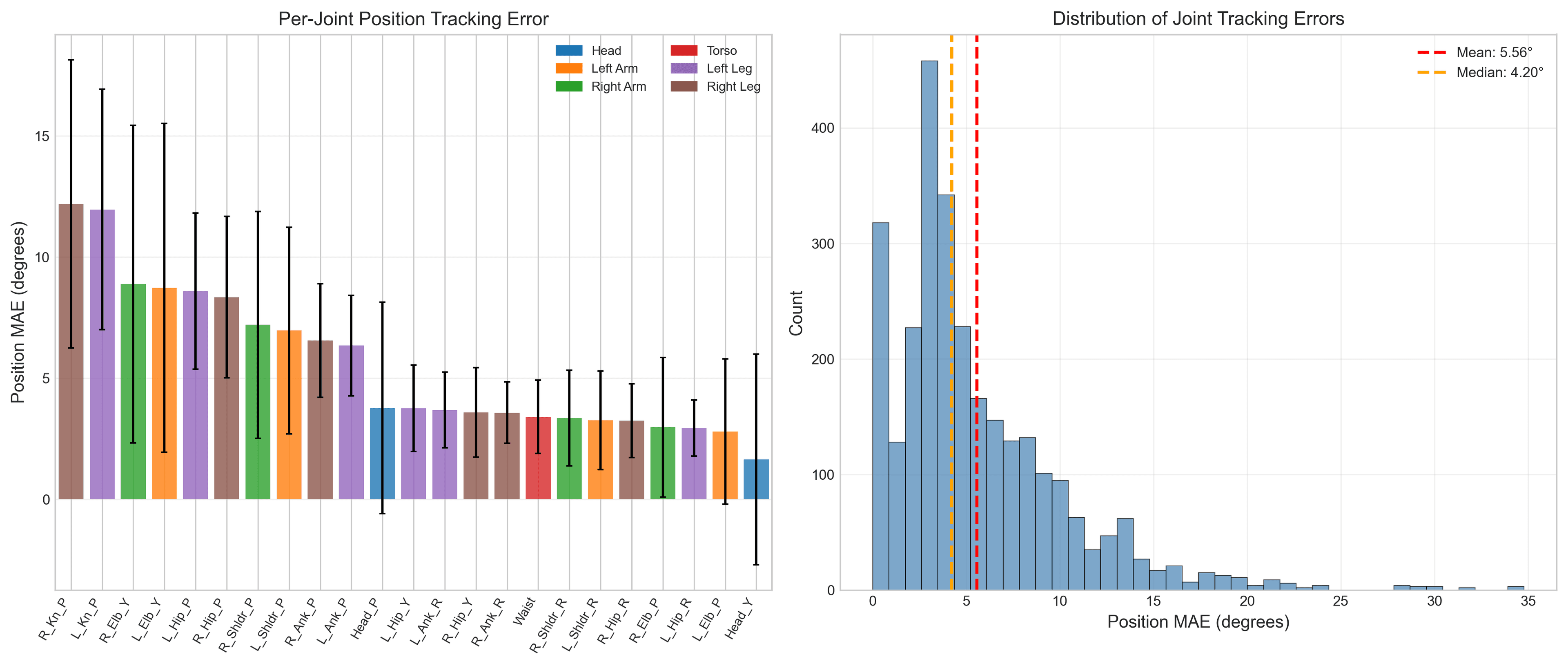
6.3 Per-Joint Analysis

Joint-specific analysis reveals heterogeneity in simulation accuracy:

6.4 Body Region Analysis

Statistical comparison: Legs vs. Arms effect size d = 0.41 (small-medium), p < 0.05. Legs show ~1.2× higher error than arms, with the difference driven primarily by knee joints.

To understand frequency-dependent divergence patterns, we performed power spectral density (PSD) analysis on both real and simulated trajectories. This reveals which frequency components are well-modeled versus poorly captured.

7.1 Frequency Band Decomposition

We decompose the spectrum into three physiologically and mechanically meaningful bands:

7.2 Spectral Divergence by Joint Category

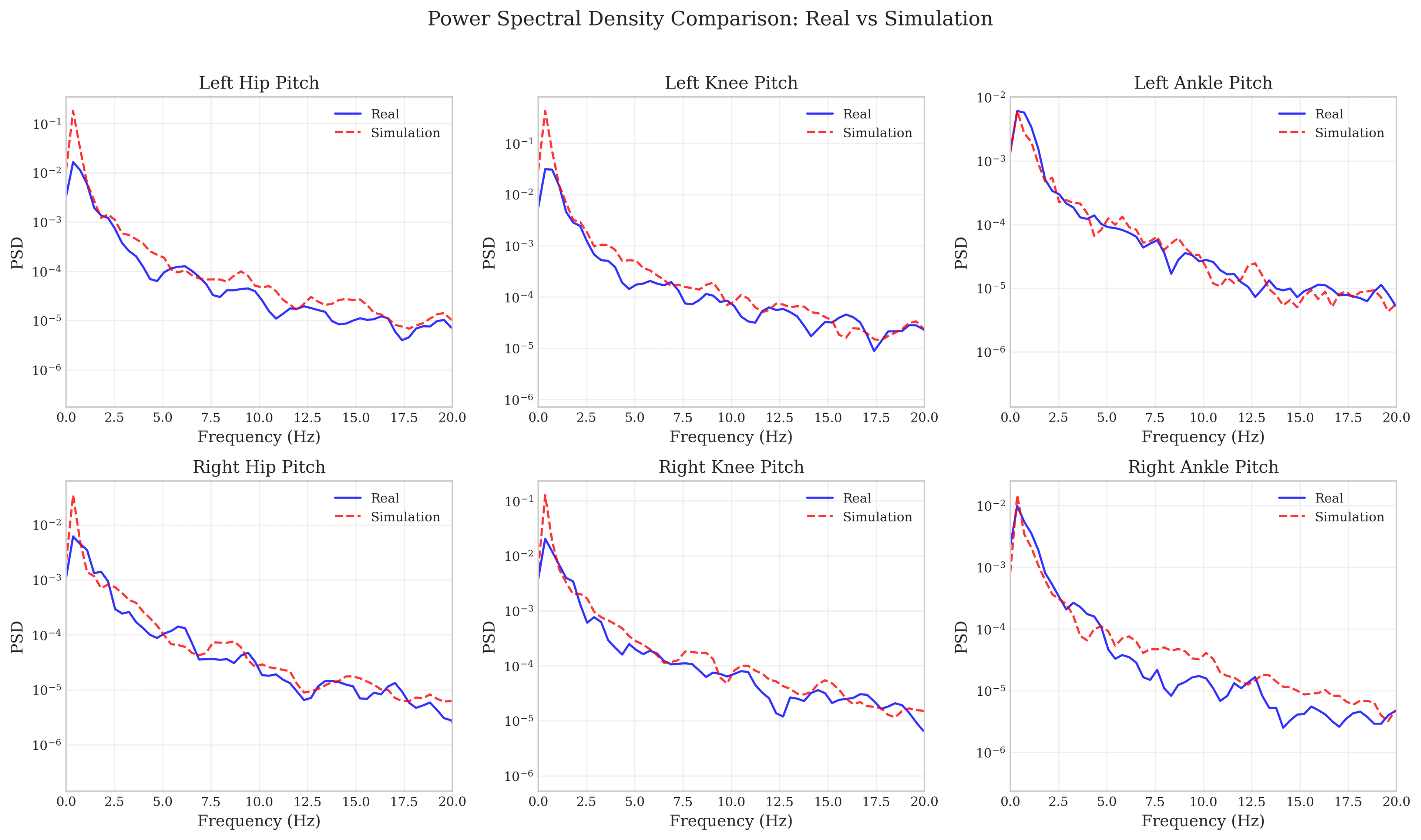
7.3 Implications for Model Improvement

The spectral analysis provides specific guidance for simulation improvement:

• Low-frequency deficit: Add noise or perturbations to reference trajectories to capture planning-level variability
• High-frequency over-damping: Reduce joint damping coefficients by 20-40%
• Head frequency mismatch: Model vestibular feedback or add IMU-driven corrections
• Contact-induced transients: The simulation misses high-frequency impact vibrations present in real foot strikes

8.1 Sources of the Sim2Real Gap

8.2 Implications for Sim2Real Transfer

Domain Randomization Ranges

Critical insight: Uniform randomization across all joints is suboptimal. Leg joints require higher randomization range than arms due to contact dynamics.

System Identification Priorities

1. Ground contact parameters (friction, stiffness, damping)
2. Knee and hip actuator dynamics (torque-speed curves, bandwidth)
3. Leg structural compliance (joint stiffness, link flexibility)
4. Arm actuator gains (lower priority given reasonable tracking)

8.3 Limitations

• Task diversity: While 123 episodes represent diverse scenarios, they are not exhaustively labeled for task-specific analysis
• Single robot: Results are specific to Booster T1; other humanoids may differ
• Position control replay: While improved over kinematic replay, closed-loop policy execution would compound errors differently
• No contact ground truth: Lack of force plates limits contact modeling analysis
• MuJoCo-specific: Results may not generalize to other physics engines (IsaacGym, PyBullet, etc.)

9.1 Summary of Findings

1. Overall position tracking error of 5.56° MAE demonstrates moderate simulation fidelity for humanoid robots
2. Leg joints show ~1.2× higher error than arms (6.7° vs 5.5° MAE), with knee pitch reaching 12° error
3. Velocity tracking is excellent (0.41 rad/s MAE) with position control replay methodology
4. Correlation varies by body region: Arms show moderate agreement (r ≈ 0.40), legs show weak agreement (r ≈ 0.15)
5. Contact modeling is the primary error source, evidenced by spatial error patterns in load-bearing joints
6. Overall gap score of 0.36 indicates good simulation fidelity suitable for policy training with appropriate domain randomization

9.2 Practical Recommendations

A. Joint Specifications

B. Dataset Statistics

C. Reproducibility

research/sim2real/
├── scripts/
│   ├── data_loader.py      # Episode data loading
│   ├── booster_t1_sim.py   # MuJoCo simulation
│   ├── sim2real_analysis.py # Main analysis
│   └── generate_figures.py  # Figure generation
├── results/
│   ├── analysis_results.json
│   └── analysis_report.txt
└── figures/
    ├── fig1_trajectory_comparison.pdf
    ├── fig2_error_distribution.pdf
    └── ...

To reproduce: cd research/sim2real/scripts && python sim2real_analysis.py

D. Citation

@article{gerra2025sim2real,
  title={Empirical Characterization of the Simulation-to-Reality
         Gap in Full-Size Bipedal Humanoid Robots},
  author={gerra},
  year={2025},
  note={Available at https://gerra.com/research/sim2real}
}